Magick
Art
Science
Religion
Blog
PentaclePower
Pranayamatron
Chaos in Art and Cultural Practice
For some it may be difficult to imagine how developments in mathematics have affected the evolution of the arts and the course of culture, let alone how they may change our own practice and how we contextualize our work. What does Math have to do with Art.
A brief look at history reveals a picture of a deep underlying relationship between the inspirations and aspirations of mathematicians and artists.
 Click for animation. |
The Greeks thought the nature of numbers and the universe was to be found in ratios. Pythagoras1 saw all things as relationships defined by the void between them 2, in the same way that the spaces between beats in a piece of music determine its rhythm and tempo. This is where we get our concept of "rationality".3
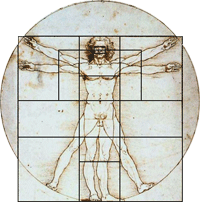
The "Golden Ratio" was particularly cherished by the Greeks and can be found in a rectangle that is constructed such that removing of a square equal to its height from one end, will leave a smaller rectangle of the same proportions at the other.
 Click for animation. |
), as he is credited with designing that Athenian Temple complex.
Further popularized in Luca Pacioli's 1509 book Divina Proportione, which was illustrated by Da Vinci and includes the famous picture of the
Vitruvian Man, this so-called "Golden Ratio" has been used since the Renaissance by artists as a guide to producing works with pleasing proportions. It has been seen as emblematic of the ideals of rationality. Ironically, is also an irrational number.
Experiments in the early 1400's by Filippo Brunelleschi (1377-1446) produced a geometrical formula for 2 dimensional representation of perspective that became the standard model for the realistic depiction of space from the Renaissance onward.
It was the development of calculus by Isaac Newton that gave the finishing touches to the Copernican heliocentric paradigm. It gave science a powerful set of predictive tools and emboldened man to believe that if these laws could be mastered the universe could be controlled.
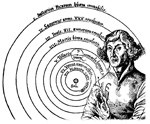
With the earth removed from the center of the universe, the church lost its monopoly on science and art and so, armed an new mechanistic world view and with a powerful set of mathematical tools that seemed to have unlimited predictive powers, the western world entered what was called the Age of Enlightenment. This was an echo of the Renaissance and of the Golden Age of Pericles, during which Phidias worked. Culture was emboldened by this paradigm to believe in the perfection of mankind through accumulation of knowledge.
So we see that for each of these time periods the cultural understanding of mathematics had both direct and indirect relations to the culture's self-expression, providing practical tools, useful paradigms and areas for further endeavor. What is the mathematical metaphor that dominates us in the information age? How does the math of today, in the early 21st century, reflect our cultural direction?
I propose that the study of complexity, also known as Chaos Theory can provide many concepts which help to give insight into the context and direction of contemporary culture, as well as technologies and methodologies for the production of valid work and theory. What tools can it provide us both practically and intellectually? Perhaps we should first ask what do we look for in such a paradigm.
A useful paradigm for artistic discourse should fulfill a few basic requirements:
It should contextualize our work in history: It should provide a historical and geographical picture of cultural phenomena that is inclusive of the diversity of human experience. It should provide explanations for developments past and present and it should be able to identify current trends and predict future developments. It should make some sense of apparent paradoxes, contradictions and disparities.
It should give direction to movements or to individuals: It should provide motivation and direction to groups, individuals and specific works, just as ideals rooted in mathematics have, throughout the ages, inspired people to believe in the power of Art to elevate and enlighten.
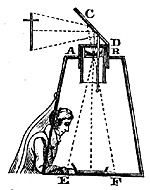
It should provide tools and technology: It should enhance or provide new avenues of expression and distribution. Just as the mathematics of optics provided optical devices that allowed painters to analyze what they saw and lead to the eventual development of the cameras and the scanners we use today.
It should provide metaphors and tools for critique and analysis: It should provide a language for understanding new concepts and relationships, just as the science of optics has given us the concepts of "focusing our attention" and "getting things in perspective". It should also have the capability of self-analysis.
It should open significant areas of endeavor: It should provide areas for artists and critics to direct their investigations and their works, in the same way that modernism opened the door to the study of contemporary life and ultimately art itself.
Chaos theory is the study of simple iterative formulae that produce complex, unpredictable results. In common usage the word "chaos" implies disorder or randomness but this sense it means an underlying, unpredictable order from which patterns emerge over time. Those patterns are called fractals and they have a number of special attributes that makes them different from Euclidean geometrical shapes. One unique aspect is that their borders are infinitely convoluted, so that it is impossible to predict if points in the vicinity are inside or outside of the shape. This complexity means that fractals occupy fractional dimensions (e.g. they can occupy a dimensionality between 2 and 3D for example) (Burger/Starbird 507).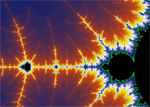
Fractals also demonstrate self-similarity at different scales. Patterns may be contiguous or have many elements that are not connected. They display infinite similarity with infinite differentiation.
The equations that create fractals do not generate patterns in a linear fashion, as in Euclidean geometry where adjacent points are determined successively, but chaotically, so that it is impossible to predetermine if subsequent iterations will generate points which will fall within the shape or not.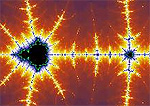
The final outcome of many iterations is radically affected by tiny changes in the initial conditions.
Chaos theory doesn't espouse a deterministic, Newtonian idea of linear causality, but one of emergence. Things can be regarded, on one level, as structures and on another as processes (Young 5). Complexity theory also denies the concept of objectivity of the observer or his/her separation from the observed (Young 11).
How can an understanding of Chaos be helpful in a cultural analysis? Culture is a non-linear dynamical system. The development and propagation of ideas is an iterative process. The repetition of concepts, verbally and concretely, forms the evolution and the canon of our culture. This process has accelerated since the development of reproduction technologies like the printing press, and is now increasing exponentially through digital information technologies. It is reasonable to expect a massively iterative system such as this to produce complex, non-linear results. How best to understand this complexity? I believe Chaos theory meets the criteria set forth earlier:
It contextualizes our work in history: The contemporary practice of referencing the distant and recent past in the forms of irony, parody, homage, reruns, remakes, takeoffs, outtakes, rip-offs, revivals, samples, loops, cover versions, re-mixes and reissues etc. is one of the defining features of Post-modernism. We inherit this practice directly from the Modernist mandate for self-analysis, which has been multiplied by the subsequent proliferation of industrial technologies for image making, replication and distribution. Fractal models allow for an understanding of the post-Internet de-centering of expertise, authority, and distribution in all realms of expression.
It gives direction to groups or to individuals: The open source movement, wikis, and distributed computing, are new forms of massively collaborative endeavor that are best understood as non-linear dynamical systems. Democratized distribution like YouTube and peer-to-peer file sharing circumvent the traditional top-down distribution models and allow the appearance "viral memes" and other emergent phenomenon. Complex systems are subject to the "Butterfly Effect", i.e. final outcomes are critically dependent on tiny changes in initial conditions, which means that all of society can be affected by the actions of individuals and small groups.
It provides tools and technology: The tools of chaos are those that allow us to produce, reproduce, alter, sample, loop, feedback and distribute information. Computers, whose sole function is to cycle thousands of times per second and store millions of iterations of ones and zeros are ideal, but so are cell phones, wireless devices, smart appliances, and samplers to name a few others. Simple chaos algorithms give realistic textures to 3D animations, encrypt sensitive data, and cut down noise in transmissions.
It provides metaphors and tools for critique: Unlike the Newtonian Paradigm, Chaos theory and cybernetics permits the concept of circular causality. Simple loops where A causes B, and B causes A are found throughout the art world, for example, in the relationship between artist, critic, and audience, between inspiration and work, and in perfomative and improvised scenarios.
The fractional dimensionality of emergent phenomena and the uncertainty of their border regions suggest what sociocyberneticist TR Young called "fractal facticity"; meaning that more than one thing can be true depending on the point of view in time and space. This approach helps to deal, in a holistic fashion, with the postmodernist de-centering of cultural discourse from the various perspectives of post-colonialist / post-structuralist / Marxist / feminist /queer / etc. theory.
A complex analysis of works is done with an eye for self-similarity at different scales, rather than linear connections and Euclidean constructions with their connotations ("right" angle, "golden" rule, getting "straight to the point" etc.). For example, Pollock's paintings have been been interpreted in terms of their fractal properties (Peterson). Emily Zants has used complexity theory to study French literature's evolution in relation to cinema (Zants).
A phenomenon like the replication, distribution and display on the Web of the self-similar frames in a QuickTime video over millions of hard drives and screens can be viewed as a vast fractal distribution intersecting both cyberspace and real space/time.
It opens significant areas of endeavor: Aside from the use of fractals for their graphical properties there are many applications where iterative systems can be applied.
Artists who produce work that demonstrates emergent behavior, like David Rokeby and Norman White, are examples of artists exploring complexity.
Artificial intelligence, massively collaborative on-line virtual spaces, ubiquitous computing and image recording with democratized distribution; these are all in the realm of complexity.
The convoluted fractal boundaries between doing and being; between real and imagined; between idea and art; between artist and viewer; between public and private; are areas of infinite richness to be explored, and what better tools than the Aesthetics of Chaos to navigate them?
Bibliography
Burger, Edward B. and Starbird, Michael The Heart of Mathematics: An invitation to effective thinking
Key College;
2 edition (August 18, 2004)
Peterson, Ivars Jackson Pollock's Fractals 1999
http://www.maa.org/mathland/mathtrek_9_20_99.html
Rokeby, David Installation Artist
http://homepage.mac.com/davidrokeby/home.html
White, Norman The Normill
http://www.normill.ca/
http://en.wikipedia.org/wiki/Pythagoreanism
http://en.wikipedia.org/wiki/Hippasus
Young TR CHAOS THEORY AND HUMAN AGENCY
http://www.critcrim.org/redfeather/chaos/chaosindex.html
Zants, Emily Chaos Theory, Complexity, Cinema and the Evolution of the French Novel
1998 Edwin Mellen Press ISBN13: 978-0-7734-8789-5
1 Pythagoras (c. 580-500 BCE), the Greek philosopher/mathematician who is known for the theorem explaining the relationship between the lengths of the side of a right triangle, also originated some profound ideas about the nature of space and time which influenced thinkers from Plato on for many centuries.
2 Aristotle (384-322 BCE) (wiki/Pythagoreanism) explains the Pythagorean concept of how Form emerges from Void by creating relationships in space and time.
The void distinguishes the natures of things, since it is the thing that separates and distinguishes the successive terms in a series. This happens in the first case of numbers; for the void distinguishes their nature.
3 So much did the Greeks cherish their rationalism that legend has it that when Hippasus discovered that the square root of 2 could not be represented as a ratio of two natural numbers, and was therefore irrational, he was drowned at sea and the information was kept secret by the Pythagoreans.
4 Clement Greenberg wrote in the 1970s that Modernism was the culmination of this social project. He said it started with the empiricism of enlightenment philosopher Immanuel Kant and manifested as a science-like self-analytical approach in the arts that culminated in Post Painterly Expressionists, like Morris Louis, who avoided the intervention of the brush by simply pouring paint on the canvas. But by then postmodernism was already underway.
5 This effect discovered by Edward Lorenz in the 1960s.When he re-ran a computer weather simulation after rounding the initial parameters off to 2 decimal places from 3 or 4 he got radically different results, leading him to say it was as if the flapping of a butterfly's wing in the forest had caused a hurricane on the other side of the world.(Burger/Starbird 490)
6 Cybernetics is the study of communication and control systems in machines and nature and important area of research is into positive and negative feedback where complex and unpredictable results are produced by self-limiting iterative systems.
7 In the introduction of her book she states:
"...novels developed techniques and structures such as fragmentation, doublings, flashbacks, or metaphorical representations that are cinematic because they engender a sense of spatial and temporal simultaneity, whereas the traditional novel is condemned to the linearity of words.(Zants)"